Finding a Point in the Line at a Specific Distance

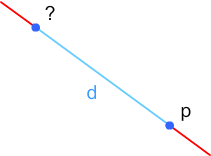
Imagine that you have a line, a point (p1) belonging to that line and you need to find a 2nd point (p2), also belonging to the line, that's at a specific distance (d) from the 1st point.
We could try to find the circle that has p1 as the center and d as the radius and check where the circle intersects with the line. But I want to try a different method that uses the line's slope and trigonometry.

First we have to take into account the equation that define the slope (m) of a line:

m =  y₂ - y₁ 
        x₂ - x₁

If we take a closer look, and remember how the trigonometric functions are tied to finding the projections of a line, we see that the slope is in fact this:

m = tan α

This means we can use the other 2 trigonometric equations that define the projections from the line to find the coordinates of the 2nd point:

sen α =  y₂ - y₁   <=> y₂ = d sen α + y₁
                d

cos α =  x₂ - x₁   <=> x₂ = d cos α + x₁
                 d

And to find how much the angle is we just need to used this:

m = tan α  <=>  α = arctan (m)